Circuitos com mais de três malhas são um pouco mais complexos para analisar, mas nesse post será mostrado como fazer a análise utilizando ferramentas como Octave e LTspice.

Quando começamos a estudar engenharia elétrica, ou um técnico na área de eletrônica, será preciso saber fazer análise de circuitos, seja com circuitos simples, com duas malhas, três malhas ou mais, além de se conhecer outras leis básicas, como leis de Kirchhoff, Thevenin, Norton, e Super posição.
Também é importante utilizar ferramentas computacionais, isso ajuda na aprendizagem, uma vez que permite calcular os valores mais rapidamente. Para isso, nós vamos fazer a análise de um circuito com cinco malhas usando o Octave e LTspice e o método convencional utilizado nas aulas de circuitos, para um comparativo.
O circuito que vamos analisar com cinco malhas aparece na figura abaixo:
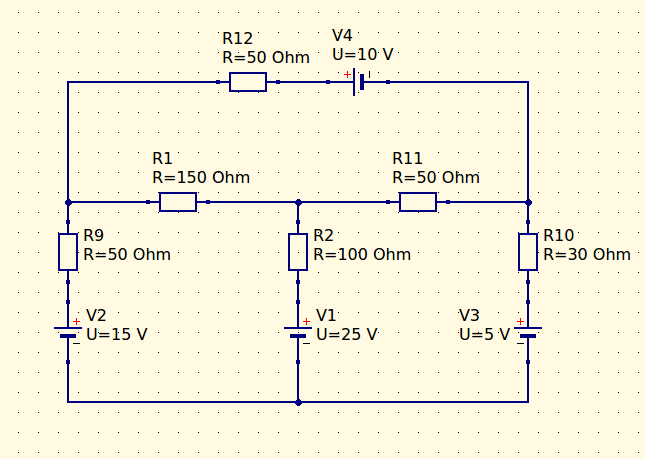
Nós precisamo encontrar os valores das correntes de malhas, e para isso vamos adotar um sentido para as correntes e vamos montar três equações com três variáveis. Na figura abaixo mostramos o sentido adotado para as três correntes nas malhas.
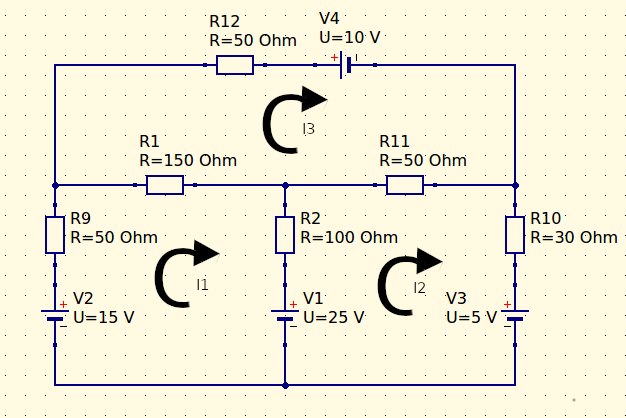
Montando as equações de malha
Vamos montar a equação para primeira malha e seguir o mesmo raciocínio para as demais malhas do circuito. Como a somas das tensões em uma malha fechada é igual a zero, e pela lei de ohm, o produto da corrente pela resistência é igual a queda de tensão no resistor, então temos:
Malha 1:
15 – 25 + (50 + 150 + 100) * I 1 – 100 * I2 – 150 * I3 = 0
300 * I1 – 100 * I2 – 150 * I3 = 10
Malha 2:
25 – 5 – 100 * I1 + (100 + 50 + 30) * I2 – 50 * I3 = 0
-100 * I1 + 180 * I2 – 50 * I3 = -20
Malha 3:
-10 – 150 * I1 – 50 * I2 + (150 + 50 + 50) * I3 = 0
-150 * I1 – 50 * I2 + 250 * I3 = 10
Escrevendo as três equações, obtemos o seguinte sistema para resolver:
300 * I1 – 100 * I2 – 150 * I3 = 10
-100 * I1 + 180 * I2 – 50 * I3 = -20
-150 * I1 – 50 * I2 + 250 * I3 = 10
Para resolver o sistema, vamos aplicar a regra de cramer.
Na matriz abaixo temos o sistema que vamos resolver.
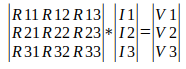
Neste caso, por exemplo, R11 é a soma de todos os resistores da malha 1, e R13 são os resistores comuns à malha 1 e 3.
Vamos calcular o delta, e depois vamos encontrar cada uma das correntes:
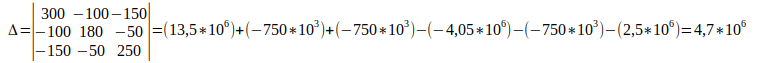
Encontrando as correntes de malha
Para calcular o valor da primeira corrente, basta substituir a coluna das tensões na primeira coluna da matriz de resistores, e calcular o determinante, e após isso dividir o valor pelo ∆.
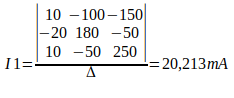
Para calcular o valor de I2, basta substituir a coluna das tensões na segunda coluna da matriz de resistores, e calcular o determinante, e após isso dividir o valor pelo ∆.
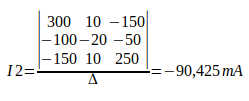
O sinal de menos indica que o sentido da corrente é contrário ao adotado inicialmente.
Para calcular o valor de I3, basta substituir a coluna das tensões na terceira coluna da matriz de resistores, e calcular o determinante, e após isso dividir o valor pelo ∆.
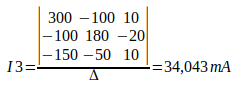
Nos cálculos que fizemos, obtemos as três correntes de malha. Agora vamos calcular as correntes que faltam:
IR1 = I3 – I1 = 34,043 – 20,213 = 13,83 mA
IR11 = I2 + I3 = 124,468 mA
IR2 = IR11 – IR1 = 110,638 mA
Scritp do Octave para análise
Com o Octave, podemos temos que fazer a mesma análise do circuito, mas vamos encontrar as três correntes de forma mais rápida, uma vez que será necessário apenas montar as equações. O código a seguir mostra a resolução do problema proposto.
clear all # Comando apaga todas as variáveis
clc # Limpa a janela de comandos
syms I1;
syms I2;
syms I3;
# R11 R12 R13 R21 R22 R23 R31 R32 R33
R = [300 -100 -150; -100 180 -50; -150 -50 250]
I = [I1; I2; I3]
V = [10; -20; 10]
I = inv(R) * VApós executar o código acima obtemos os seguintes resultados:
Symbolic pkg v2.9.0: Python communication link active, SymPy v1.5.1.
R =
300 -100 -150
-100 180 -50
-150 -50 250
I = (sym 3×1 matrix)
⎡I₁⎤
⎢ ⎥
⎢I₂⎥
⎢ ⎥
⎣I₃⎦
V =
10
-20
10
I =
0.020213
-0.090426
0.034043Simulando o circuito com LTSpice
A seguir vamos fazer a mesma análise do circuito acima, só que no LTSpice, e uma tabela com os valores da simulação.
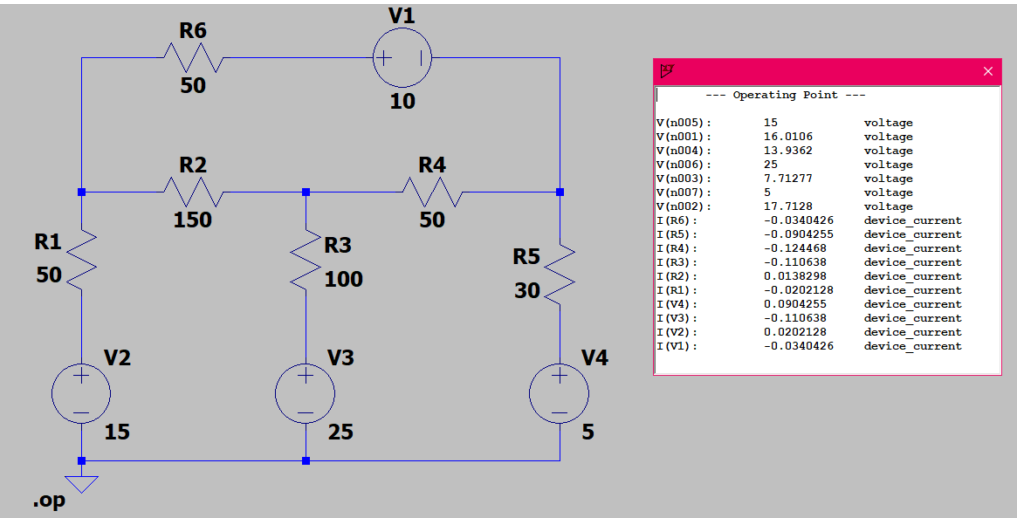
Para concluir, as simulações e ferramentas computacionais permitem um melhor aprendizado, uma vez que ajudam a resolver problemas de circuitos mais facilmente. Observem que o LTSpice fornece praticamente todos os valores de tensão e corrente para cada componente.
O mais importante, é que aprendendo a utilizar essas ferramentas, além de ajudar na resolução de problemas de circuitos, também ajuda muito na hora de fazer um projeto eletrônico mais elaborado.

