Neste post será feito uma introdução a função seno, e mostrados alguns detalhes sobre o comportamento de indutores e capacitores em corrente alternada.

A função seno está muito presente em circuitos de corrente alternada, e também em sinais utilizados em amplificadores, uma vez que qualquer sinal pode ser gerado através da soma de sinais senoidais. Outro detalhe importante, é que a função seno é uma função periódica, que se repete no decorrer do tempo. Abaixo temos a forma básica da função seno:
y (x) = sen (x)
Onde x é ângulo da função seno.

Em engenharia, se utiliza os ângulos em π radianos, e em algumas calculadoras, como Geogebra e Desmos, também utilizam π radianos. Para converter, basta fazer (ângulo * π /180) para obter em π radianos, abaixo segue uma tabela com os principais ângulos:

Ângulo em graus	Ângulo em π radianos
0º	0
30º	π/6
60º	π/3
90º	π/2
120º	2 π/3
180º	π
270º	3 π/2
360º	π

A seguir temos a forma da função seno, obtido através da ferramenta online Desmos:

Propriedades da função seno

Em Engenharia Elétrica, normalmente se faz análises de sinais de corrente e tensão, normalmente se faz análise da amplitude do sinal, da frequência, e da defasagem em relação a outro sinal.
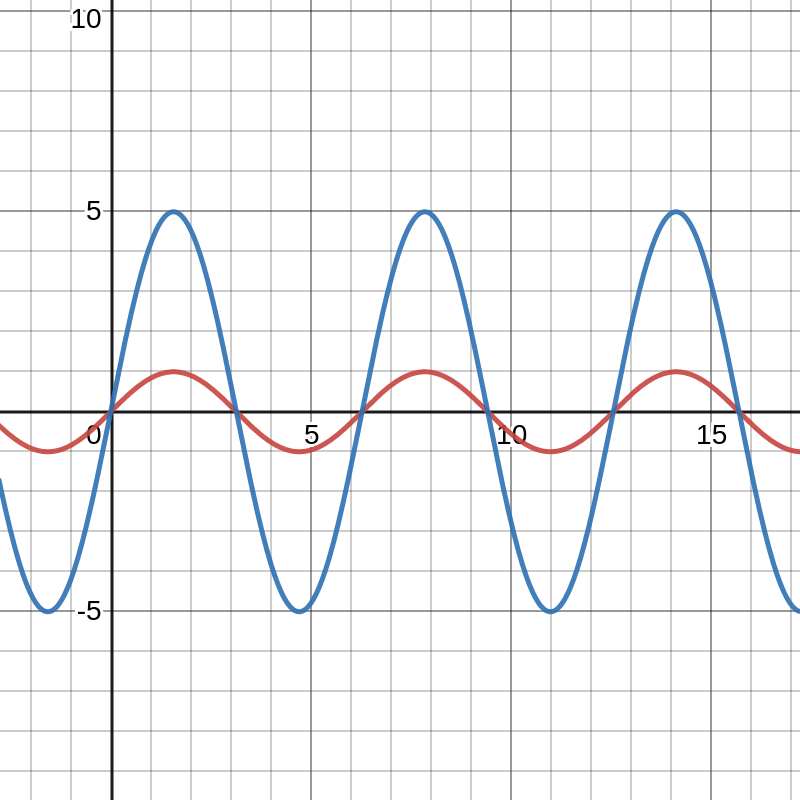
Inicialmente vamos verificar a amplitude de um sinal, que pode ser alterada, mudando o valor de A:
y (x) = A * sin (x)

Em azul, é possível ver um sinal, que pode ser, por exemplo, uma tensão de 5 Vp e em vermelho uma tensão de 1 Vp, ou 10 Vpp e 2 Vpp. A função do sinal em azul é y (x) = 5 * sin (x).
Agora, vamos supor que precisamo de um sinal cinco vezes mais rápido, como na figura abaixo:

O sinal em azul é cinco vezes mais rápido do que em vermelho, para isso multiplicamos o valor de x em cinco vezes, y (x) = sin (5 * x).
Mas podemos ter um sinal mais lento, por exemplo, como o sinal abaixo em azul, que é obtido da seguinte maneira, y (x) = sin ( x / 2):

Outro sinal utilizando a função seno que é interessante, seria um sinal que começa com uma velocidade baixa, e aumenta no decorrer do tempo, para isso podemos fazer y (x) = sin (x²).

Agora vamos supor, que fosse necessário que o sinal oscilasse entre 10 e 0, e não entre -5 e 5, como mostra o gráfico abaixo:

Para isso, devemos somar 5 ao nosso sinal, a função do gráfico em azul fica assim: y (x) = 5 * (x) + 5, caso fosse menos 5, o sinal irá começar em -5, ir até zero, e atingir -10 em seguida.
Agora será mostrado uma das partes mais interessantes para área de Engenharia Elétrica, que trata do deslocamento de fase entre dois gráficos de função seno. Observem o gráfico a seguir:

Observem quem o gráfico em azul começou bem antes do que o gráfico em vermelho, assim podemos dizer que o gráfico em azul está adiantado em relação ao gráfico em vermelho.
y (x) = 5 * (x) -> Vermelho
z (x) = 5 * (x + π/2) -> Azul.
A função em azul, também pode ser escrito como z (x) = 5 * cos (x).
Por que isso é importante?

Capacitores e indutores

O que vem a seguir é apenas um comentário sobre capacitores e indutores, nada muito complexo.

Em circuitos elétricos e em eletrônica é muito comum encontrar os três principais componentes passivos, resistores, capacitores e indutores.
Os resistores e os capacitores são mais comuns, pois se consegue construir esses componentes mais facilmente e com boa precisão se comparados aos indutores.

Os capacitores e indutores são componentes que desempenham melhor suas funções em sinais que variam com o tempo, que é o caso de sinais senoidais.
Em circuitos de corrente contínua, esses componentes não são tão interessantes. Um capacitor, vai apenas se carregar, até atingir o nível de tensão DC da fonte; e o indutor vai funcionar como um eletroímã, e isso depende muito também da quantidade de espiras do circuito.

Para finalizar, as características dos indutores e dos capacitores, está relacionado ao deslocamento de fase entre a tensão e corrente. Como no gráfico que discute deslocamento de fase.

De forma a deixar claro, e não gerar nenhuma confusão, segue abaixo como fica para o indutor e para o capacitor.
Indutor: v (t) = sin (t + π/2); i (t) = sin (t) -> A corrente está atrasada em 90º em relação a tensão;
Capacitor: v (t) = sin (t); i (t) = sin (t + π/2) -> A tensão está atrasada em 90º em relação a corrente.
No gráfico acima, para temos:
Indutor: Tensão em Azul e corrente em vermelho;
Capacitor: Tensão em Vermelho e corrente em azul.

Uma analogia, levando em consideração o símbolo do indutor, é que a corrente teria que dar muitas voltas em relação a tensão que já foi aplicado aos seus terminais, por isso a corrente está atrasada em relação a tensão, e no capacitor acontece o contrário, isso pode ajudar a lembrar.