Neste post será feito a análise de circuitos com capacitores e indutores, e para comprovar os resultados obtidos será feito a simulação do circuito utilizando o LTSpice.

No exercício a seguir precisamos calcular o valor do capacitor C1, de forma que a tensão e a corrente da fonte de alimentação fiquem com a mesma fase.
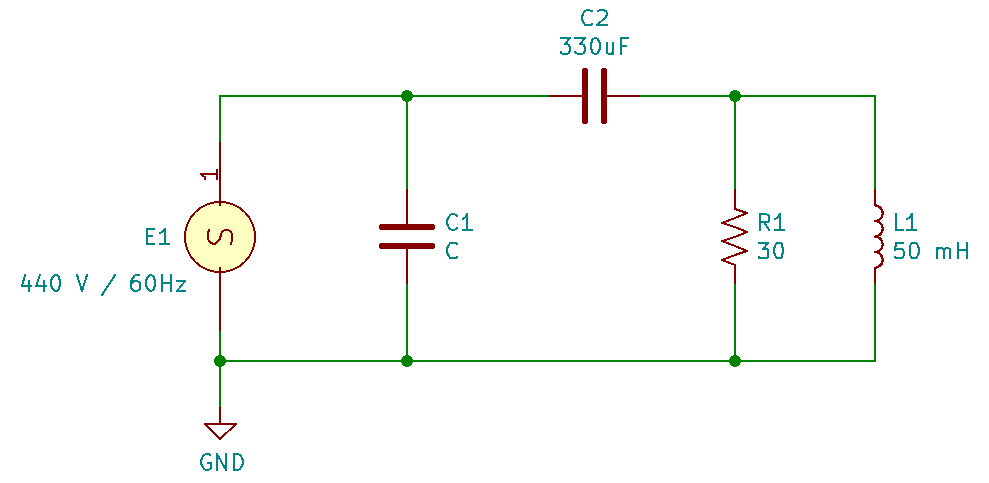
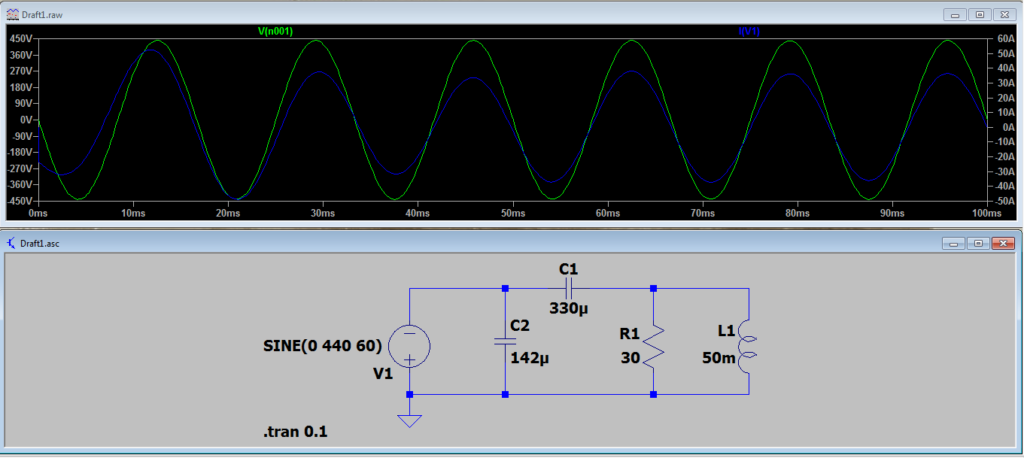
Para isso, vamos considerar o circuito da figura a seguir, que possui uma fonte de alimentação com uma tensão de 440 V, com um frequência de 60 hertz; dois capacitores, um resistor e um indutor:

O primeiro passo, é calcular as reatâncias capacitivas e indutivas do circuito, para o capacitor C2 e para o indutor L1, como segue abaixo:

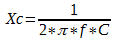
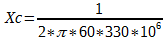
Xc = -8,04j ou Xc = -8j [Ω]

Para o indutor teremos o seguinte:

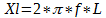
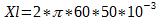
Xl = 18,85j [Ω]

Em circuitos, utilizamos a letra ‘j’ para expressa que o número em questão faz parte do conjunto dos números complexos.
Vamos fazer a análise de circuito, de uma maneira muito semelhando quando analisamos circuitos apenas com resistores, mas vamos utilizar números complexos, pois estamos analisando circuitos que utilizam capacitores e indutores.
Primeiramente, vamos analisar o resistor R1 em paralelo com o indutor, então nós temos:

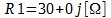
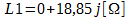
Quando trabalhamos com resistores em paralelo, por exemplo, R1 e R2, para encontrar o resistor equivalente da associação, nós fazemos os produto de R1 por R2, divido pela soma de R1 por R2.
Será feito dessa mesma maneira para encontrar a impedância equivalente da associação do resistor R1 com o indutor L1.

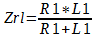
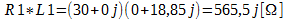
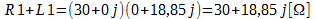
Como Zrl é uma divisão de números complexos, essa divisão pode ser facilmente se convertendo os dois números para forma polar.
Entretanto, vamos utilizar outro método, multiplicando o numerador e denominador pelo conjugado do denominador, como mostrado a seguir:

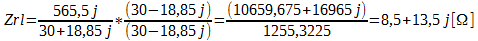
Agora vamos obter o seguinte circuito:

Como C2 está está em série com impedância Zrl, vamos subtrair o -8j para encontrar a impedância em paralelo com C1.

Z1 = 8,5 + (13,5j – 8j) [Ω]
Z1 = 8,5 + 5,5j [Ω]

A corrente que passa por essa impedância deve estar em fase com a impedância do capacitor C1.
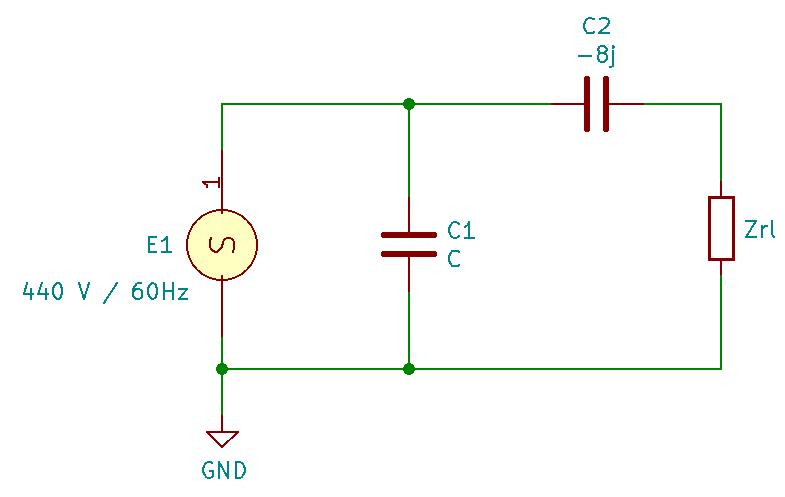
Para encontrar a corrente, devemos dividir a tensão da fonte pela impedância Z1, como pode ser observado a seguir:

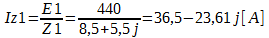
A parte que deve estar em fase com a fonte, é parte imaginária, então vamos utilizar o valor de -23,61j para encontrar o valor da reatância capacitiva, para que a corrente fique em fase com a tensão, e logo após aplicar a fórmula da reatância capacitiva para encontrar o valor do capacitor.

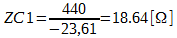
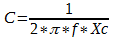
O capacitor deve ter um valor de 142,3 uF para que a corrente da fonte esteja em fase com a tensão.

Simulação no LTSpice

Vamos fazer uma simulação computacional, da análise de circuitos que fizemos acima, e para isso vamos utilizar o LTSpice.
Na figura que segue mostra a simulação no LTSpice, com os valores calculados de acordo com o post acima:

Agora vamos alterar a frequência da fonte de alimentação, e verifique o que acontece com os sinais da corrente e da tensão da fonte:

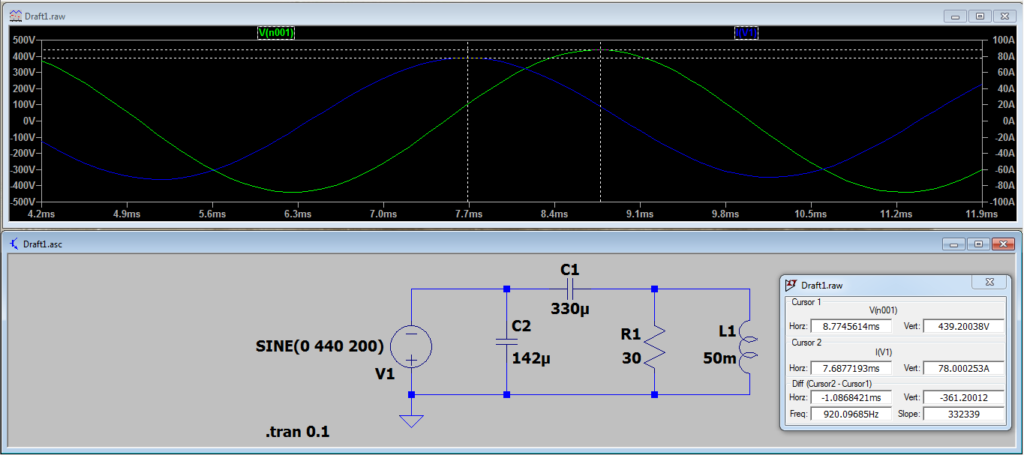
A corrente em azul, está adiantada em relação ao sinal da tensão em verde.
Para calcular o ângulo de defasagem do sinal da corrente em relação tensão, podemos aplicar a seguinte equação:

Se for obter a defasagem em graus utilize a equação da esquerda, e caso prefira em π radianos utilize da esquerda.
O denominador se refere ao período do sinal, ou seja, devemos utilizar o inverso do frequência para encontrar o seu valor, no nosso caso temos T = 1 / 200, portanto T = 5 ms. Abaixo segue o valor do ângulo de defasagem da corrente em relação a tensão.

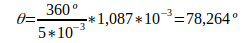
Isso é tudo, e até o próximo post!

chave pix para doações: wantronics@wantronics.com.br