
A expansão em frações parciais consiste em se expandir uma fração em uma soma de frações. Esse recurso é muito utilizado nos cursos de engenharia, na matéria de controle e servomecanismos, pois permite que seja aplicado a transformada de Laplace de uma forma mais fácil.
O objeitvo é fazer a expansão em frações parciais com Octave, mas primeiramente vamos fazer a expansão em frações parciais sem a utilização de ferramentas computacionais, para conhecermos o processo passo a passo.
Vamos expandir em frações parciais a seguinte função de transferência:
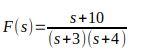
O que queremos fazer, para facilitar na aplicação da transformada de Laplace, é expandir a função de transferência acima, em uma soma de duas frações, como mostrado logo abaixo:
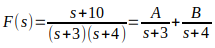
O que temos que fazer inicialmente, é encontrar uma valor que anule o valor do denominador (s+3), e outro valor que anule o denominador (s+4), ou seja:
s + 3 = 0, resolvendo a equação temos s = -3
s + 4 = 0, resolvendo a equação temos s = -4
Após esse processo, devemos substituir os valores na função de transferência, mas de forma que o valor encontrado não zere o denominador, pois senão haverá uma divisão por zero.
Por exemplo, para encontrar o valor de A, removemos do denominador a parte (s + 3), e substituímos o valor que foi encontrado em (s+4), e para encontrar o valor de B, removemos a parte (s + 4), e substituímos o valor que foi encontrado em (s + 3).
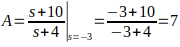
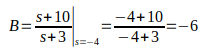
Agora temos a resposta.
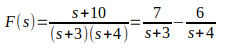
Para verificar se a resposta está correta, basta somar as duas frações, e tirar a prova real, mas vamos utilizar o Octave, uma ferramenta com as mesmas funcionalidades do Matlab para verificar se nossa resolução está correta.
Script do Octave para expansão em frações parciaisi
Agora vamos fazer a expansão em frações parciais com Octave, para isso utilizem o link no final do post para acessar o Octave Online.
% DEN = (s + 3) * (s + 4) = s² + 4s + 3s + 12 = s² + 7s + 12
NUM = [1 10];
DEN = [1 7 12];
[r, p, k] = residue(NUM, DEN)
Observem que no Octave, para montar a matriz do denominador, devemos fazer a operação distributiva entre (s + 3) e (s + 4).
Como exercício, acessem o Octave Online verifiquem se a resposta encontrada condiz com o esperado, e verifiquem com a ajuda do comando help, como funciona o recurso residue utilizado no script acima.
Até o próximo post!

