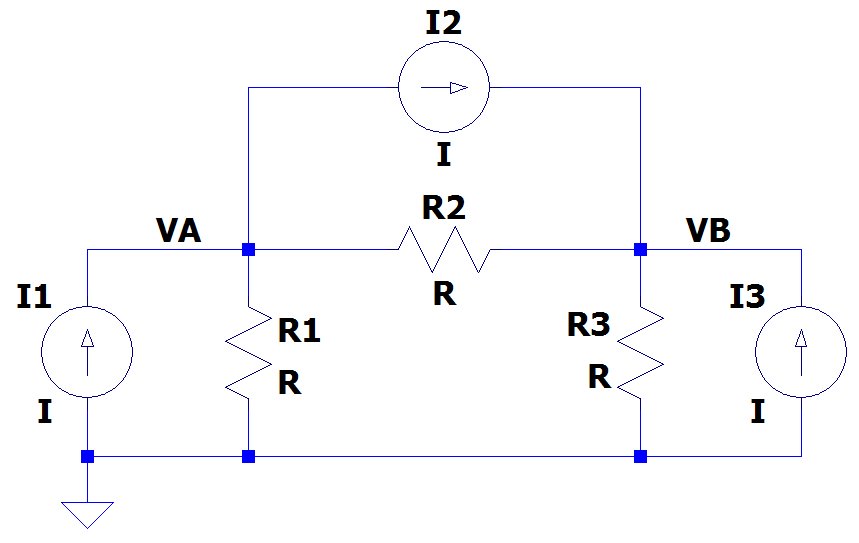
Neste post será feito uma análise de circuitos pelo método dos nós, utilizando duas abordagens diferentes. Uma das análise será feito de uma forma mais passo a passo, e vai envolver uma quantidade maior de manipulações das equações, e a outra forma será feito de forma mais direta e mais interessante.
Após a análise do nosso circuito pelos dois métodos, vamos utilizar o Octave Online para resolver as equações e obter os valores que estamos procurando, e também vamos fazer um simulação utilizando o LTSpice, para comprovar que os valores obtidos em nossos cálculos estão corretos.
Análise de circuitos pelo método dos nós – Primeiro método
Antes de iniciar a análise do circuito, vale ressaltar que o método dos nós é mais utilizado quando nosso circuito utiliza fontes de corrente, e com isso podemos encontrar os valores da tensão nos nós do circuito.
O circuito que vamos analisar é mostrado abaixo com os todos os valores que precisamos:
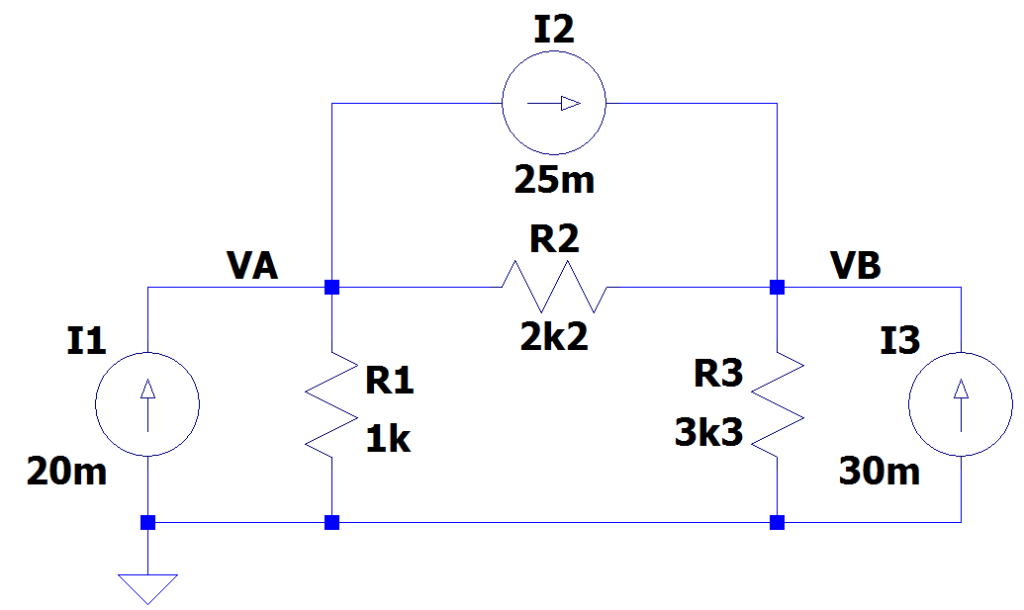
Inicialmente vamos convencionar que uma corrente que entra em um nó será positiva, e uma corrente que saí de um nó será negativa.
Vamos iniciar nossa análise escrevendo as duas equações para o nó VA e para o nó VB:
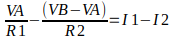
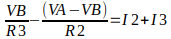
O que temos é uma equação simultânea com duas incógnitas. Antes de substituir os valores, vale a pena simplificar as duas equações acima afim de se obter duas equações mais fáceis de se trabalhar. Vamos aplicar o mmc nas duas equações, e com isso remover os denominadores.
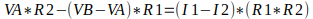
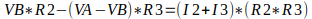
Observe, por exemplo, na primeira equação que o mmc é igual a R1 multiplicado por R2, e quando fazemos operações com frações, dividimos o mmc pelo denominador e multiplicamos por todos os numerador da equação, então a primeira linha vai ficar como VA*R2 – (VB-VA)*R1 = (I1-I2) *(R1*R1). O mesmo se aplica a VB.
Agora, vamos aplicar a propriedade distributiva da multiplicação do lado esquerdo das nossas equações:
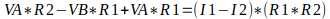

Podemos colocar em evidência VA na primeira equação e VB na segunda equação, obtendo assim duas equações com duas variáveis, como mostrado abaixo:

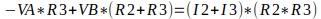
Após esses passos, podemos substituir os valores do circuito nas equações, e encontrar o valor de VA e de VB.
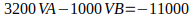
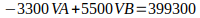
Utilizando determinantes, calculamos o valor de delta, depois os valores de VA e de VB.
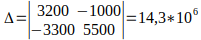
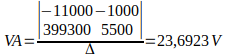

Análise de circuitos pelo método dos nós – Segundo método
A segunda maneira de fazer a mesma análise, mas sem utilizar as frações é utilizar os valores das condutâncias dos resistores, que nada mais é do que o inverso da resistência.
Para calcular o valor inverso de uma grandeza, basta fazer 1 divido pelo valor da grandeza, por exemplo, se precisamos saber a condutância de um resistor de 100 ohms, podemos fazer 1 divido por 100, e obtemos 10 mS (dez mili Siemens).
A condutância dos resistores são as seguintes:
Para o resistor R1: G1 = 1 mS;
Para o resistor R2: G2 = 0,4545 mS;
Para o resistor R3: G3 = 0,303 mS.
Agora, ao invés de começar por todas as equações, e fazer as simplificações das frações, podemos simplesmente utilizar equações sem frações, o que vai poupar muito trabalho e tempo para resolução do exercício, acompanhe:
Agora basta fazer uma análise semelhante a análise que é feita quando se faz análise de malhas.


Substituindo os valores temos:
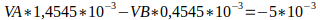
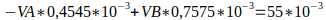
Utilizando determinantes, vamos encontrar o valor de delta, depois os valores de VA e de VB.


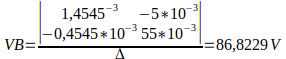
Nos dois casos foi utilizado o método dos nós para fazer a análise do circuito, e é possível verificar que obtemos os mesmos resultados, houve apenas uma pequena variação de arredondamento das casas decimais.
Encontrando os valores com Octave online
Abaixo segue o script para ser executado no Octave, para encontrar os valores das correntes pelo método dos nós como apresentado no primeiro método, execute no Octave online e compare com os valores obtidos nos cálculos acima.
# Análise pelo método dos nós - Primeiro método
clear all # Comando apaga todas as variáveis
clc # Limpa a janela de comandos
# Valores que queremos encontrar de VA e VB
syms VA;
syms VB;
# Fontes de corrente
I1 = 20e-3;
I2 = 25e-3;
I3 = 30e-3;
# Resistores
R1 = 1e3;
R2 = 2.2e3;
R3 = 3.3e3;
# VA * (R1 + R2) - VB * R1 = (I1 - I2) * (R1 * R2)
# - VA * R3 + VB * (R2 + R3) = (I2 + I3) * (R2 * R3)
R = [(R1 + R2) -R1; -R3 (R2 + R3)]
I = [(I1 - I2) * (R1 * R2); (I2 + I3) * (R2 * R3)]
V = [VA; VB]
V = inv(R) * I
Agora vamos fazer a mesma análise, só que desta vez utilizando condutâncias, vamos apenas modificar o código acima para que utilize condutância no lugar de resistência:
# Análise pelo método dos nós - Segundo método
clear all # Comando apaga todas as variáveis
clc # Limpa a janela de comandos
# Valores que queremos encontrar de VA e VB
syms VA;
syms VB;
# Fontes de corrente
I1 = 20e-3;
I2 = 25e-3;
I3 = 30e-3;
# Resistores
G1 = 1 / 1e3;
G2 = 1 / 2.2e3;
G3 = 1 / 3.3e3;
# VA * (G1+G2) - VB * G2 = (I1 - I2)
# -VA * G2 + VB * (G2 + G3) = (I2+I3)
R = [(G1 + G2) -G2; -G2 (G2 + G3)]
I = [(I1 - I2); (I2 + I3)]
V = [VA; VB]
V = inv(R) * I
Os resultados obtidos no Octave são praticamente os mesmos nos dois casos, nos primeiros exemplos foi utilizado uma calculadora, e os valores foram arredondados até a quarta casa decimal.
Simulação do circuito no LTSpice
Para comprovar que os valores obtidos pela análise dos nós está correto, abaixo é mostrado a simulação do circuito, com os valores pelo software LTSpice.
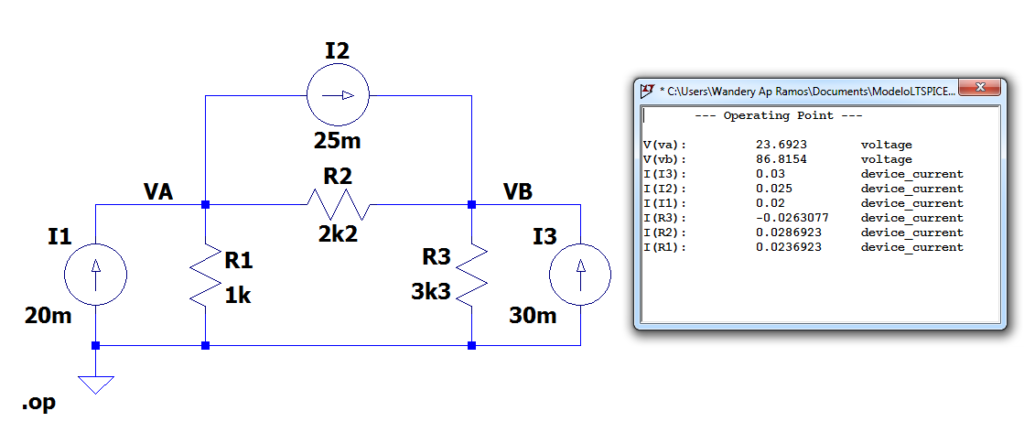
Os valores obtidos na simulação e os valores calculados são bem próximos.
Explore outros artigos no site da Wantronics.
https://wantronics.com.br/2021/04/07/analise-de-circuitos-com-capacitor-e-indutor/
https://wantronics.com.br/2021/04/02/circuito-com-tres-malhas-uma-analise-com-octave-e-ltspice/

