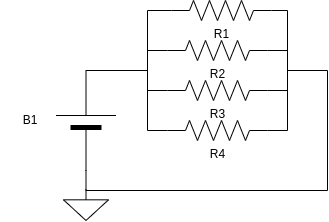
Neste post vamos analisar circuitos com resistores em paralelo, deduzir as equações e analisar alguns circuitos.
Em circuitos eletrônicos é muito comum encontrar associações de resistores, seja como um circuito divisor de tensão, ou divisor de corrente, ou em casos onde durante um projeto crítico se calculou um determinado valor mas esse valor não é encontrado comercialmente, daí surge a necessidade de se fazer uma combinação de resistores para se obter o valor desejado.
Vamos verificar como obtemos as equações para as associações resistivos.
Resistor e uma fonte de tensão
Quando temos um circuito simples com apenas um resistor ou uma lâmpada ligado em uma bateria, circula uma corrente através do nosso circuito, como mostrado abaixo:
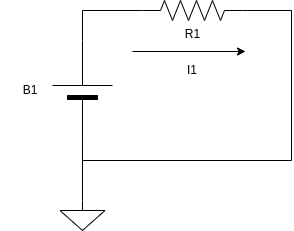
Conhecendo o valor da tensão da bateria B1, que é dado em volts, e conhecendo o valor ôhmico do resistor, que é dado em ohms, e aplicando a lei de ohm, podemos facilmente encontrar o valor da corrente que circula pelo nosso circuito, como mostrado pela equação abaixo:
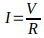
Com isso podemos encontrar o valor da corrente do nosso circuito, e já conseguimos muitos dados relevantes sobre o nosso circuito.
Mas vamos supor que foram adicionados mais resistores ao circuito como mostrado abaixo, como fazemos para encontrar as outras informações o sobre o nosso circuito?

Resistores em paralelo
Vamos supor que a nossa fonte de tensão é perfeita, e que o valor de sua tensão é mesmo para os dois circuitos apresentados até o momento.
Como é possível observar pela figura, todos os resistores estão conectados ao terminal positivo e ao terminal negativo da bateria B1, ou seja, todo os resistores estão submetidos ao mesmo nível de tensão. Com isso podemos encontrar o valor da corrente em cada resistor facilmente, apenas dividindo o valor da tensão pelo valor da resistência de cada resistor, como mostrado abaixo:
IR1 = VB1 / R1
IR2 = VB1 / R2
IR3 = VB1 / R3
IR4 = VB1 / R4
Mas como podemos encontrar o valor da resistência equivalente do nosso circuito? Vamos observar a imagem abaixo, que mostra a corrente total drenada pela bateria e a corrente que atravessa cada resistor do circuito:
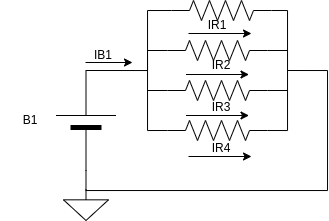
Podemos concluir que a corrente total drenada pelo circuito é igual soma das correntes que atravessa cada resistor, como mostrado abaixo:
IB1 = IR1 + IR2 + IR3 + IR4
Substituindo na equação acima, as equações das correntes, e já isolando o valor da tensão VB1, obtemos a seguinte equação:
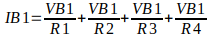
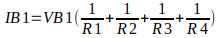
Dividindo os dois lados da equação por VB1, obtemos a seguinte equação:
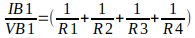
Mas observem que não obtemos o valor da resistência, pois quando dividimos corrente por tensão obtemos condutância, que é a unidade equivalente ao inverso da resistência. O importante neste ponto é notar como se obtém o valor da equação que calcula resistores em paralelo, então para encontrar o valor da resistência equivalente em paralelo temos a seguinte equação:
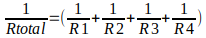
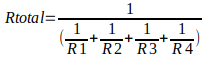
Com isso foi apresentado uma maneira de se deduzir as equações que são apresentadas para encontrar os valores de associações de resistores. É importante notar que assimilando como deduzir as equações, não precisamos necessariamente decorar todas as equações.
Exercícios
Calcular o valor da resistência equivalente, da corrente em cada resistor, e a corrente total do circuito abaixo:
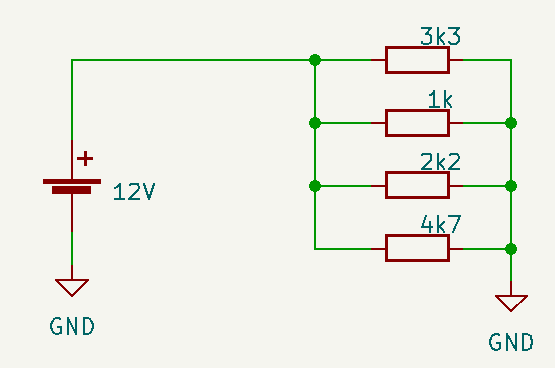
Para calcular o valor da resistência equivalente podemos fazer a soma dos inversos das resistências, e depois calcular o inverso. Mas existe uma forma mais fácil de realizar esse cálculo e obtermos o mesmo resultado, para isso podemos separar em grupos de dois resistores, fazer a multiplicação e dividir pela soma, assim obteremos o resultado para um par de resistores, e depois podemos fazer isso até não sobrar mais resistores.
Rta = (3k3 * 1k) / (3k3 + 1k) = 767,44Ω;
Rtb = (2k2 * 767,44Ω) / (2k2 + 767,44Ω) = 568,96Ω;
Req = (4k7 * 568,96Ω) / (4K7 + 568,96Ω) = 507,52Ω.
Obtemos uma resistência equivalente de 507,52Ω. Observem que em uma associação em série o valor da resistência equivalente é maior do que a maior resistência do circuito, e que em uma associação de resistores em paralelo a resistência equivalente é menor do que a menor resistência do circuito. Apenas para fins de comparação, caso o cálculo da resistência equivalente fosse feito utilizando o método da soma dos inversos:
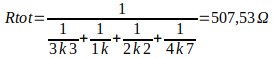
Com o valor da resistência equivalente podemos calcular a corrente que é drenada da fonte de alimentação:
Itotal = 12 / 507,52Ω = 23,64 mA
Agora vamos calcular o valor da corrente em cada resistor:
I3k3 = 12 / 3300 = 3,63 mA;
I1k = 12 / 1000 = 12 mA;
I2k2 = 12 / 2200 = 5,45 mA;
I4k7 = 12 / 4700 = 2,55 mA.
Vamos somar a corrente que cada resistor consome e observar o que valor que obtemos:
I = 3,63 mA + 12 mA + 5,45 mA + 2,55 mA = 23,63 mA
Até o próximo post.

