Neste post vamos resolver algumas equações usando capacitores e resistores. Vamos ver exemplos de circuitos em corrente contínua.

Capacitores e resistores em fonte de tensão contínua

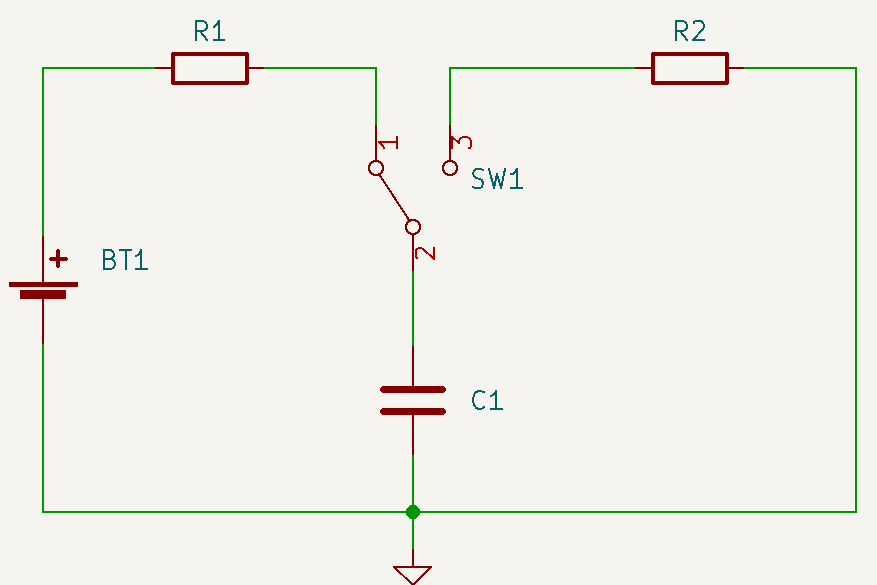
O primeiro circuito que vamos avaliar é um circuito de carga e descarga de capacitores em fonte de tensão contínua. Abaixo é apresentado um circuito que pode faz a carga e descarga do capacitor, a depender da posição da chave SW1:

Quando a chave está na posição 1, a bateria carrega o capacitor através de R1, e quando a chave está na posição 3, o capacitor é descarregado através do resistor R2.

O tempo em segundos de carga e descarga do capacitor é determinado pelo produto do valor da capacitância pela resistência, como apresentado na equação abaixo:

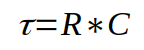
Para que o capacitor se carregue ou se descarregue completamente, são necessários 5 constantes de tempo. Então para um resistor de 1 kΩ e um capacitor de 1 μF, o tempo para o capacitor atingir a carga máxima será de 5 ms.

O capacitor vai ser carregar até aproximadamente o valor da fonte de alimentação, por exemplo, se a fonte de alimentação for de 12 V, o capacitor vai ser carregar até um valor próximo de 12 V.

Agora vamos ver as equações para carga do capacitor.

Carga do capacitor

Considerando o capacitor inicialmente descarregado, quando ligamos a chave na posição 1, vai começar a circular uma corrente que vai carregar o capacitor. A corrente no instante inicial será máxima, e será determinada pela razão entre a tensão da fonte e o valor do resistor R1.

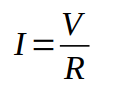
A corrente vai cair no decorrer do tempo de forma exponencial, de acordo com a carga no capacitor. A tensão no resistor R1 também vai cair conforme o capacitor se carregar.

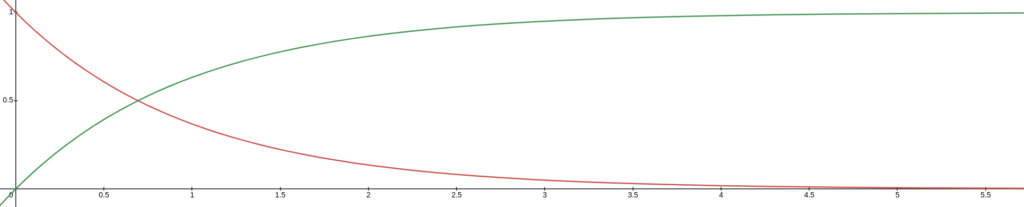
Abaixo é apresentado o gráfico para um circuito de carga que possuí constante de tempo igual a um segundo e tensão de alimentação igual a 1 V. Em verde temos a curva de tensão no capacitor, e em vermelho é apresentado a curva de tensão no resistor:

Para determinar o valor da tensão no capacitor podemos utilizar a seguinte a equação:

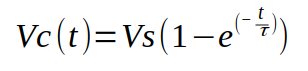
Onde:
Vc é tensão no capacitor em função do tempo;
Vs é a tensão na fonte de alimentação;
t é o tempo decorrido onde se deseja saber o valor da tensão no capacitor;
τ é constante de tempo determinado através do produto entre o valor do capacitor e resistor.

Observem que a tensão no capacitor Vc não será maior do que a tensão da fonte Vs.

Para determinar a tensão no resistor, usamos a equação abaixo:

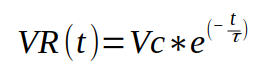
Onde:
VR é tensão no resistor em função do tempo;
Vs é a tensão na fonte de alimentação;
t é o tempo decorrido onde se deseja saber o valor da tensão no capacitor;
τ é constante de tempo determinado através do produto entre o valor do capacitor e resistor.

Para encontrar a corrente em um determinado instante de tempo, existem duas possibilidades, uma consiste em encontrar o valor da tensão no resistor naquele instante de tempo, e depois aplicar a lei de ohm para encontrar a corrente.

A outra maneira de encontrar a corrente é através da equação abaixo:

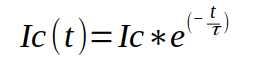
Onde:
Ic é corrente no capacitor em função do tempo;
Is é a corrente máxima do circuito, determinado pelo valor da tensão dividido pelo resistor R1;
t é o tempo decorrido onde se deseja saber o valor da tensão no capacitor;
τ é constante de tempo determinado através do produto entre o valor do capacitor e resistor.

Descarga do capacitor

Agora vamos mudar a posição da chave SW1 para posição 3 e vamos descarregar o capacitor.

Abaixo é apresentado o gráfico para um circuito de descarga que possuí constante de tempo igual a um segundo e tensão no capacitor é igual a 1 V. A tensão no capacitor e no resistor no momento da descarga serão os mesmos, e o gráfico ficará como mostrado abaixo:

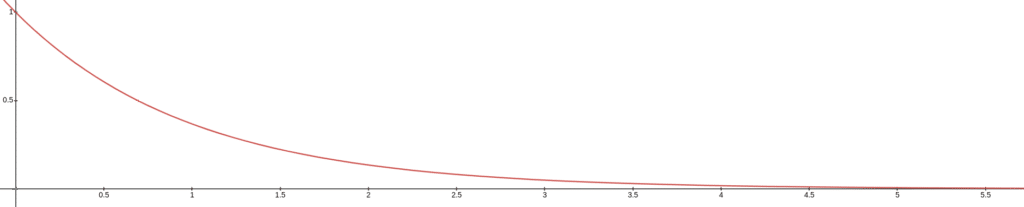
Para determinar o valor da tensão no capacitor podemos utilizar a seguinte a equação:

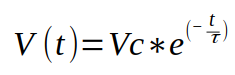
Onde:
V é tensão no capacitor em função do tempo;
Vc é a tensão inicial do capacitor;
t é o tempo decorrido onde se deseja saber o valor da tensão no capacitor;
τ é constante de tempo determinado através do produto entre o valor do capacitor e resistor.

Para determinar a tensão no resistor, usamos a equação abaixo:

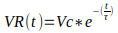
Onde:
VR é tensão no resistor em função do tempo;
Vc é a tensão inicial do capacitor;
t é o tempo decorrido onde se deseja saber o valor da tensão no capacitor;
τ é constante de tempo determinado através do produto entre o valor do capacitor e resistor.

Para encontrar a corrente em um determinado instante de tempo, existem duas possibilidades, uma consiste em encontrar o valor da tensão no resistor naquele instante de tempo, e depois aplicar a lei de ohm para encontrar a corrente.

A outra maneira de encontrar a corrente é através da equação abaixo:

Onde:
Ic é corrente no capacitor em função do tempo;
Is é a corrente máxima do circuito, determinado pelo valor da tensão inicial do capacitor dividido pelo resistor R2;
t é o tempo decorrido onde se deseja saber o valor da tensão no capacitor;
τ é constante de tempo determinado através do produto entre o valor do capacitor e resistor.

Exercício resolvido

Abaixo é apresentado um exemplo de um exercício resolvido:

É isso pessoal, neste post vimos capacitores e resistores em série, e até o próximo post.