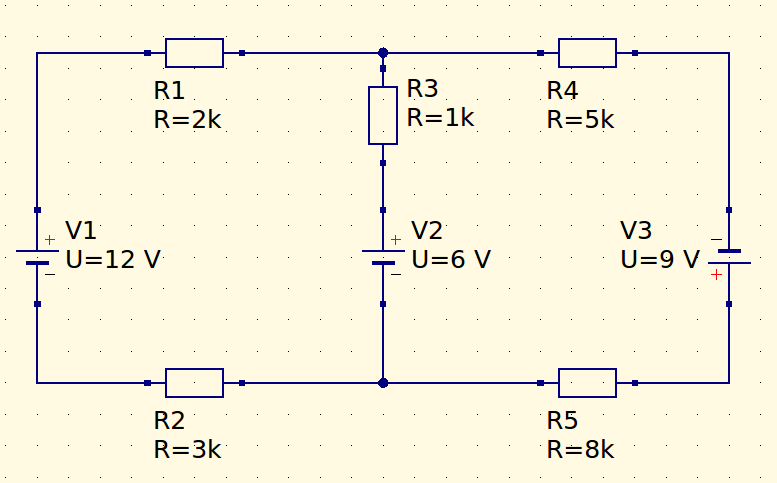
No seguinte post, vamos fazer a análise do circuito mostrada na figura acima. Vamos encontrar todas as correntes, e com isso podemos encontrar a tensão em cada um dos resistores.

Primeiramente, vamos definir um sentido para as duas correntes de malha, I1 e I2, e através do sentido das correntes, vamos obter duas equações, com duas incógnitas.

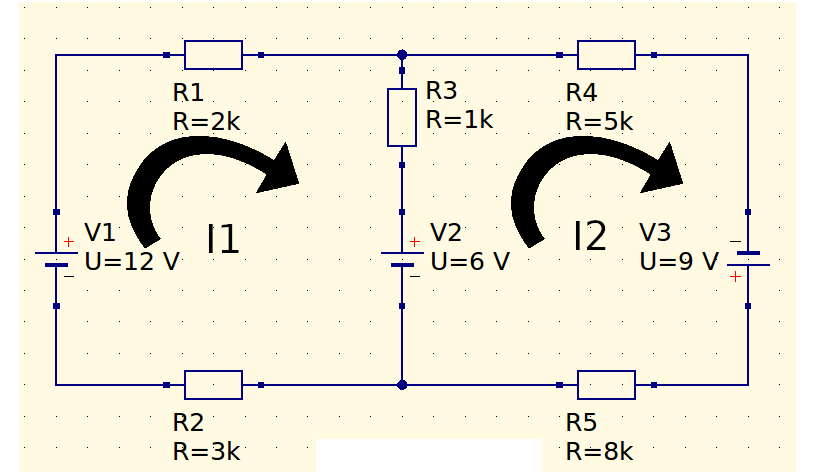
Montando as equações

Vamos escrever a equação para malha da esquerda, e depois vamos escrever a equação para a malha da direita, seguindo o sentido da corrente indicado pelas setas. Mas caso se obtenha algum valor de corrente com sinal negativo, isso indica que o sentido da corrente adotado está incorreto. A partir da fonte de 12 V, acompanhando o sentido da corrente temos:

Malha 1:
12V – 6V – (2k + 1k + 3k) * I1 + (1k) * I2 = 0;
(6k) * I1 – (1k) * I2 = 6

Para malha 2, vamos partir da fonte de 6V.

Malha 2:
6V + 9V + (1k) * I1 – (1k + 5k + 8k) * I2 = 0
-(1k) * I1 + (14k) * I2 = 15

Escrevendo as duas equações, obtemos:
6k * I1 – 1k * I2 = 6
-1k * I1 + 14k * I2 = 15

Resolvendo o sistema de equações com duas variáveis para encontrar as correntes

Agora temos um sistema com duas incógnitas e com duas equações, para resolver esse sistemas temos algumas opções, isolar uma das variáveis, por cramer, ou até mesmo utilizar uma ferramenta computacional como o Octave. Em um post anterior foi feito por cramer, neste vamos isolar uma das variáveis, para isso vamos multiplicar a segunda equação por 6, e vamos somar à primeira e com isso podemos zerar o valor de I1, e encontrar a corrente I2:
6k * I1 – 1k * I2 = 6
-1k * I1 + 14k * I2 = 15 *(6)

6k * I1 – 1k * I2 = 6
-6k * I1 – 84k * I2 = 90

Somando as duas equações podemos encontrar o valor de I2:
83k * I2 = 96
I2 = 96 / 83k = 1,1566 mA

Substituindo o valor de I2 em qualquer uma das duas equações, podemos encontrar o valor de I1:
6k * I1 – 1k * (1,1566 mA) = 6
6k * I1 = 6 + 1,1566
I1 = 7,1566 / 6k = 1,1928 mA

Como os sinais no resultado calculado das correntes não foi negativo, isso indica que o sentido escolhido está correto. Para encontrar a corrente que passa através do resistor R3, podemos fazer a diferença entre a corrente I1 e a corrente I2:
I3 = I1 – I2
I3 = 1,1928 mA – 1,1566 mA
I3 = 36,2 uA

Para calcular a tensão, pode ser utilizado a calculadora da lei de ohm, basta multiplicar o valor da corrente que circula através do resistor, pelo valor ôhmico do resistor, e com isso obtemos a tensão sobre o resistor.
Com isso, concluímos essa parte da análise do circuito, agora vamos utilizar as ferramentas computacionais.

Scritp do Octave para análise

Copie e cole o script abaixo no Octave, ou no Octave online e verifique o resultados obtidos para nossa análise de circuito.

clear all # Comando apaga todas as variáveis
clc # Limpa a janela de comandos

syms I1;
syms I2;
syms I3;

#    R11  R12  R21 R22
R = [6000 -1000; -1000 14000]
I = [I1; I2]
V = [6; 15]

I = inv(R) * V

Simulação no LTSpice

Abaixo é mostrado os resultados da análise do mesmo circuito utilizando o LTSpice:

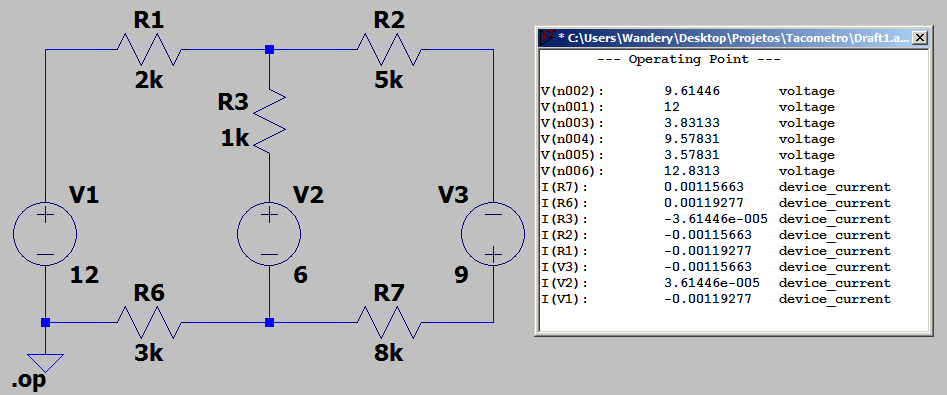
Com isso podemos encontrar a tensão e a corrente em todos os resistores do circuito, e também podemos utilizar ferramentas computacionais para verificar os resultados obtidos.

Vejam também a análise de um circuito mais complexo no link do post abaixo: