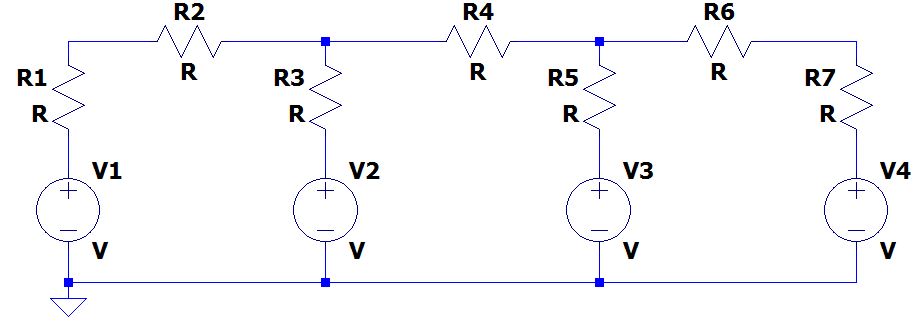
Neste post vamos resolver um exercício de análise circuitos por análise de malhas. O objetivo é resolver o exercício passo a passo, e após isso utilizar ferramentas computacionais para auxiliar na resolução do problema, e também para verificar se os valores obtidos estão de corretos.
Na figura abaixo é mostrado o circuito com os valores dos componentes:
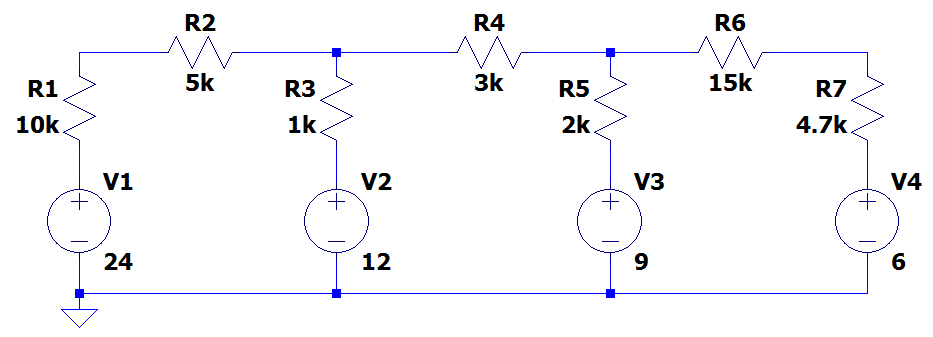
Primeiramente vamos definir um sentido para corrente nas três malhas principais do circuito, como mostrado abaixo:
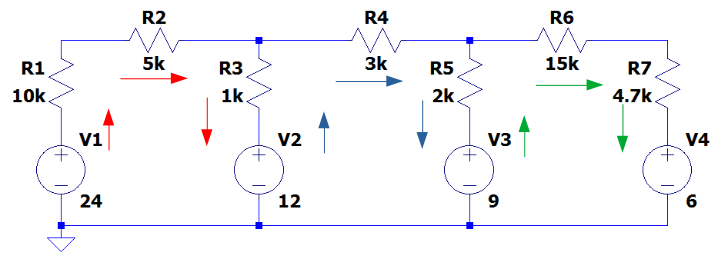
O sentido da corrente nos ajudar a escrever as equações para encontrar o valor da corrente. Entretanto, caso seja encontrado algum valor de corrente negativo, isso apenas quer dizer que o sentido adotado acima está invertido.
Escrevendo as equações de malha
Vamos montar a equação para primeira malha e seguir o mesmo raciocínio para as demais malhas do circuito. Como a somas das tensões em uma malha fechada é igual a zero, e pela lei de ohm, o produto da corrente pela resistência é igual a queda de tensão no resistor, então temos:
Malha 1 :
24V – 12V + (10k + 5k + 1k)*I1 – (1k)*I2 – 0 * I3= 0
(16k) * I1 – 1K (I2) – (0) * I3 = -12
Malha 2:
12V – 9V – (1k)*I1 + (1k + 3k + 2k)*I2 – (2k)*I3 = 0
(-1K)*I1 + (6k)*I2 -(2k)*I3 = -3
Malha 3:
9V – 6V – (0)*I1 – (2k)*I2) + (2k + 15k + 4.7k)*I3 = 0
(0)*I1 – (2k)*I2 + (21,7k)*I3 = -3
Escrevendo as três equações, obtemos o seguinte sistema para resolver:
(16k) * I1 – 1K (I2) – (0) * I3 = -12
(-1K)*I1 + (6k)*I2 -(2k)*I3 = -3
(0)*I1 – (2k)*I2 + (21,7k)*I3 = -3
Para resolver o sistema, vamos aplicar a regra de cramer.
Na matriz abaixo temos o sistema que vamos resolver.
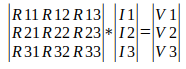
Neste caso, por exemplo, R11 é a soma de todos os resistores da malha 1, e R13 são os resistores comuns à malha 1 e 3.
Vamos calcular o delta, e depois vamos encontrar cada uma das correntes:
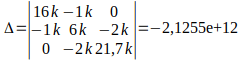
Encontrando as correntes de malha
Para calcular o valor da primeira corrente, basta substituir a coluna das tensões na primeira coluna da matriz de resistores, e calcular o determinante, e após isso dividir o valor pelo ∆.
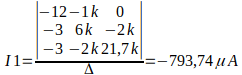
Para calcular o valor de I2, basta substituir a coluna das tensões na segunda coluna da matriz de resistores, e calcular o determinante, e após isso dividir o valor pelo ∆.
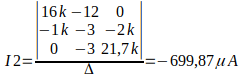
Para calcular o valor de I3, basta substituir a coluna das tensões na terceira coluna da matriz de resistores, e calcular o determinante, e após isso dividir o valor pelo ∆.
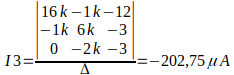
O valor negativo indica que a corrente está em sentido contrário ao adotado inicialmente.
Com todos os valores de corrente, podemos encontrar as correntes em R3 e em R5:
IR3 = I1 + I2 = 793,74 uA – 669,87 uA = 93,87 uA
IR5 = I2 – I3 = 669,87 uA – 202,75 uA = 497,12 uA
Encontrando os valores com Octave online
Com o Octave, podemos temos que fazer a mesma análise do circuito, mas vamos encontrar as três correntes de forma mais rápida, uma vez que será necessário apenas montar as equações. O código a seguir mostra a resolução do problema proposto.
clear all # Comando apaga todas as variáveis
clc # Limpa a janela de comandos
syms I1;
syms I2;
syms I3;
# R11 R12 R13 R21 R22 R23 R31 R32 R33
R = [16e3 -1e3 0; -1e3 6e3 -2e3; 0 -2e3 21.7e3]
I = [I1; I2; I3]
V = [-12; -3; -3]
I = inv(R) * V
Após executar o código acima obtemos os seguintes resultados:
Symbolic pkg v2.9.0: Python communication link active, SymPy v1.5.1.
R =
16000 -1000 0
-1000 6000 -2000
0 -2000 21700
I = (sym 3×1 matrix)
⎡I₁⎤
⎢ ⎥
⎢I₂⎥
⎢ ⎥
⎣I₃⎦
V =
-12
-3
-3
I =
-7.9374e-04
-6.9987e-04
-2.0275e-04
Simulando o circuito com LTSpice
A seguir vamos fazer a mesma análise do circuito acima, só que no LTSpice, e uma tabela com os valores da simulação.
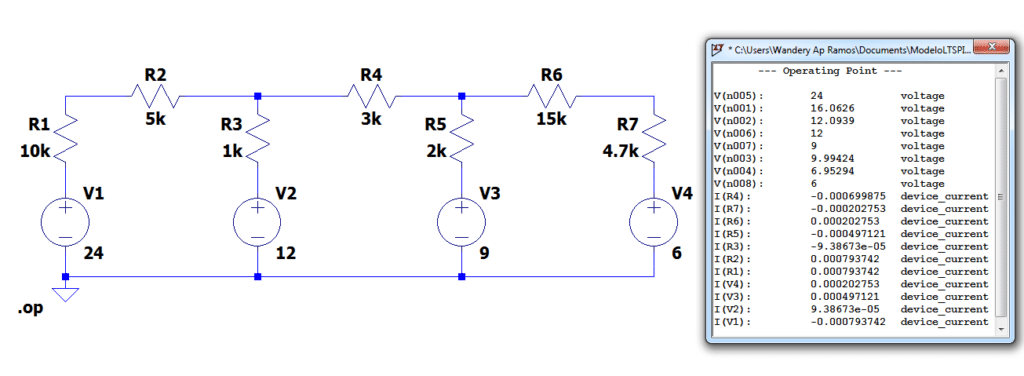
Para concluir, apesar deste exercício ser semelhante a outro já resolvido aqui no blog, podemos observar a importância do uso de ferramentas computacionais, seja para resolver exercícios propostos em sala de aula, ou para resolver problemas que possam surgir no dia a dia.
Observem que o LTSpice fornece praticamente todos os valores de tensão e corrente para cada componente.
O mais importante, é que aprendendo a utilizar essas ferramentas, além de ajudar na resolução de problemas de circuitos, também ajuda muito na hora de fazer um projeto eletrônico mais elaborado.

