
Neste post vamos aprender sobre a álgebra booleana, alguns postulados, propriedades e resolver alguns exercícios.
As portas lógicas apresentadas no post anterior são partes importantes da eletrônica digital, mas quando projetamos circuitos eletrônicos normalmente utilizamos muitas portas lógicas combinadas para realizar uma determinada tarefa, ou resolver uma determinada expressão lógica.
Entretanto, após obter uma expressão lógica a partir de uma tabela verdade, muitas vezes é possível aplicar a álgebra de Boole para obter uma expressão lógica mais simples e com isso um circuito mais simples também.
Isso é muito útil, uma vez que permite que se utilize um número de portas lógicas utilizadas em um circuito.
Primeiramente vamos conhecer os postulados, propriedades, identidades e o teorema de De Morgan
Álgebra Booleana
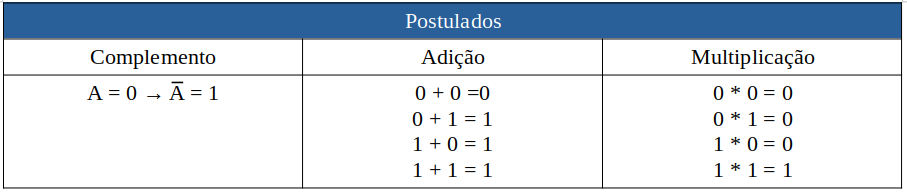
Abaixo é apresentado uma tabela com todos os postulados da Álgebra de Booleana:
Abaixo é apresentado uma tabela com todas as identidades da Álgebra de Booleana:

Abaixo é apresentado uma tabela com todas as propriedades da Álgebra de Booleana:

Abaixo é apresentado uma tabela com os teoremas de De Morgan:

E abaixo é mostrado uma tabela com três identidades que são usadas para facilitar na resoluções de alguns problemas:

Exercícios resolvidos
Com todas estas informações agora é possível resolver alguns exercícios e verificar a importância da álgebra booleana na eletrônica digital, vamos começar a resolver a seguinte expressão lógica:
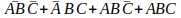
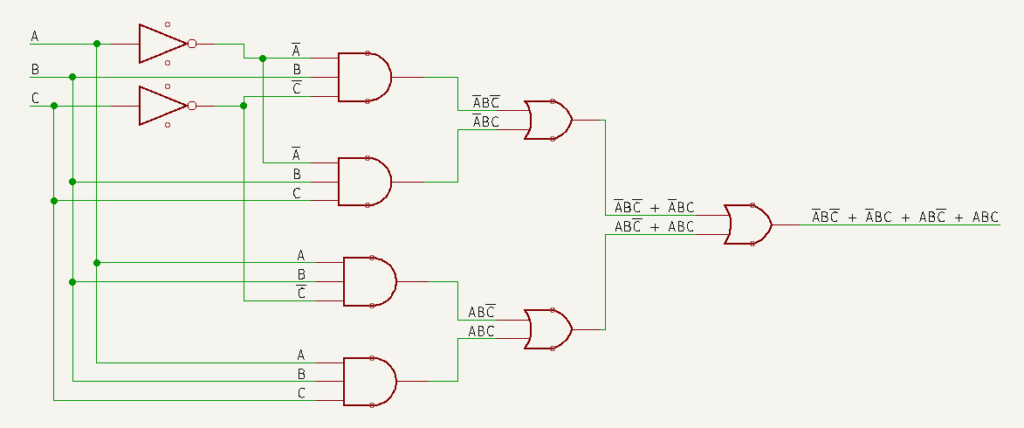
Abaixo é mostrado o circuito equivalente para a expressão lógica acima, composto por quatro portas lógicas E, duas portas lógicas inversoras e três porta lógica OU:
Agora utilizando os conhecimentos de fatoração e com o auxílio das tabelas apresentados vamos agrupar primeiramente as entradas ‘As’ e ‘As barra’, como mostrado abaixo:
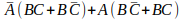
Agora podemos agrupar também os termos comuns dentro dos parênteses, como mostrado abaixo:
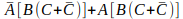
Consultando a tabela de identidades é possível verificar que quando uma entrada é somada com a mesma entrada invertida o resultado é igual a 1, então podemos substituir as somas dos dois ‘Cs’ por 1, e novamente consultando a mesma tabela, quado temos uma entrada multiplicada por 1, obtemos ela mesmo. Com isso nossa expressão lógica ficará como mostrado abaixo:
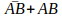
Com a expressão acima já conseguimos reduzir o número de portas lógicas de 9 para apenas 4 portas lógicas, mas ainda é possível fazer mais uma simplificação da expressão acima, colocando a entrada B em evidência, como mostrado abaixo:
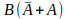
Agora temos uma situação equivalente ao que aconteceu na segunda etapa do exercício, ou seja, temos a entrada A somada com a entrada A invertida, com isso obteremos um valor igual a 1, e multiplicado pela entrada B, obtemos a própria entrada B.
Com a prática é possível aplicar a álgebra boolena sem a utilização das tabelas e regras apresentadas acima, mas é necessário que se resolva vários exercícios que explorem todos os aspectos das tabelas apresentadas.
Conclusão
Com isso é possível verificar a importância de se saber aplicar a álgebra booleana para simplificação de circuitos lógicos, pois partimos de um exemplo que utilizava várias portas lógicas e que poderia ser substituído por um cabo que conecta a entrada B na saída do circuito.
Como dito anteriormente isso é muito importante, pois pode economizar recursos na hora de implementar um circuito, e o mesmo princípio também pode ser aplicado na hora de programar um microcontrolador, ou computador que utiliza muitas tomadas de decisão, de forma a reduzir o tamanho do código, diminuindo assim o uso de memória.
Existem outros métodos e ferramentas que auxiliam na simplificação de expressões lógicas e circuitos combinacionais, como os mapas de Karnaugh, e ferramentas computacionais que podem fazer a simplificação de foram fácil e eficiente, mas o importante é ter isso em mente na hora de fazer um projeto eletrônico.

