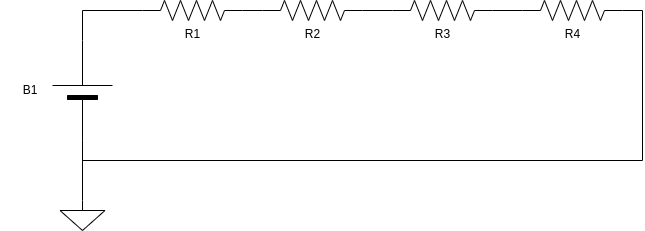
Neste post vamos analisar circuitos com resistores em série, deduzir as equações e analisar alguns circuitos.
Em circuitos eletrônicos é muito comum encontrar associações de resistores, seja como um circuito divisor de tensão, ou divisor de corrente, ou em casos onde durante um projeto crítico se calculou um determinado valor mas esse valor não é encontrado comercialmente, daí surge a necessidade de se fazer uma combinação de resistores para se obter o valor desejado.
Vamos verificar como obtemos as equações para as associações resistivos.
Resistor e uma fonte de tensão
Quando temos um circuito simples com apenas um resistor ou uma lâmpada ligado em uma bateria, circula uma corrente através do nosso circuito, como mostrado abaixo:
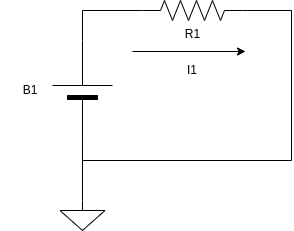
Conhecendo o valor da tensão da bateria B1, que é dado em volts, e conhecendo o valor ôhmico do resistor, que é dado em ohms, e aplicando a lei de ohm, podemos facilmente encontrar o valor da corrente que circula pelo nosso circuito, como mostrado pela equação abaixo:
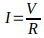
Com isso podemos encontrar o valor da corrente do nosso circuito, e já conseguimos muitos dados relevantes sobre o nosso circuito.
Mas vamos supor que foram adicionados mais resistores ao circuito como mostrado abaixo, como fazemos para encontrar as outras informações o sobre o nosso circuito?

Resistores em série
Vamos supor que a nossa fonte de tensão é perfeita, e que o valor de sua tensão é mesmo para os dois circuitos apresentados até o momento.
O que podemos fazer é manipular a equação da lei de ohm que foi apresentado acima e encontrar uma equação onde seja possível calcular ao valor da tensão ao invés de calcular a corrente, isso é facilmente obtido como mostrado pela equação abaixo:
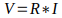
Outro ponto importante a se observar neste momento é que a corrente que circula por todos os resistores tem o mesmo valor, ou seja, a corrente não se divide entre os elementos do circuitos, como mostrado pela figura abaixo:
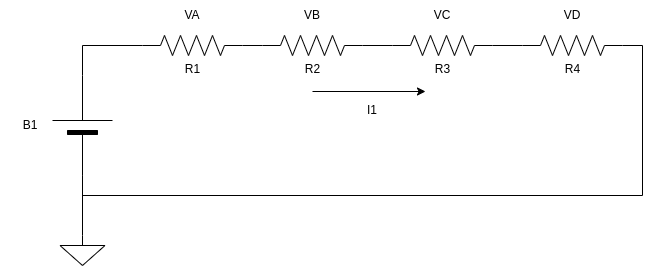
Observem que foram utilizados valore de tensão que vão de VA até VD, isso porque em circuitos com resistores em série o que acontece é que a tensão se divide entre os resistores, e a soma das quedas de tensão deve ser igual a tensão fornecida pela fonte de alimentação, ou seja:
VB1 = VA + VB + VC + VD
Utilizando a equação da lei de ohm mostrada acima, onde é possível encontrar o valor da tensão com os valores dos resistores e com o valor da corrente obtemos:
VB1 = (R1 * I) + (R2 * I) + R3 * I) + (R4 * I)
Como a corrente que atravessa o circuito tem o mesmo valor e vale I, podemos colocar a corrente em evidência e chegamos a seguinte equação:
VB1 = I * (R1 + R2 + R3 + R4)
Com isso temos que o valor de n resistores ligados em série é igual a soma do valor ôhmico de suas resistências.
Exercícios resolvidos
Determinar o valor da resistência equivalente e o valor da corrente e da queda de tensão em cada resistor da figura abaixo:
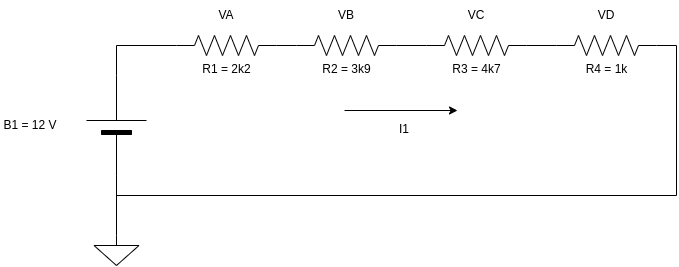
Primeiramente vamos somar o valor de todos os resistores, para obter o valor da resistência total do circuito:
Rtotal = 2k2 + 3k3 + 4k7 + 1k = 11k2
Para obtermos o valor da corrente basta dividir a tensão pelo valor da soma de todos os resistores do circuito:
I1 = VB1 / Rtotal = 12 / 11k2 = 1,071 mA
Com o valor da corrente podemo encontrar o valor da queda de tensão em cada resistor, como mostrado abaixo:
VA = 2,356 V;
VB = 3,534 V;
VC = 5,034 V
VD = 1,071 V
Somando todas as tensões obtemos:
Vtotal = 2,356 + 3,534 + 5,034 + 1,071 = 11,995 V, ou seja, 12 V.
Exercício 2
Determinar o valor do resistor R3 para que a corrente no circuito seja igual a 1,5 mA.
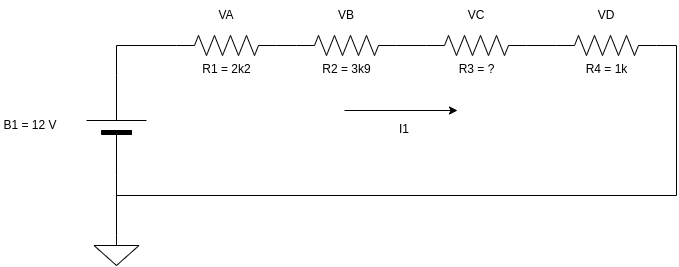
Esse exercício pode parecer mais intimidador, mas vamos resolvê-lo. O que precisamos saber neste caso é valor da resistência equivalente total, e como temos o valor da tensão da fonte de alimentação, e o valor da corrente que precisamos que circule pelo circuito, vamos encontrar o valor da resistência total, como mostrado abaixo:
Rtotal = 12 / 1,5 mA = 8k
Como temos os valores de R1, R2 e R4, basta somar os valores desses três resistores e subtrair da resistência equivalente total, e com isso determinamos o valor de R3:
R3 = 8k – (2k2 + 3k9 + 1k) = 900 Ω
Exercício 3
Com o circuito da figura abaixo encontre o valor da tensão em R3, deduzindo a equação do divisor de tensão resistivo:

Muitos alunos perguntam qual é a equação para calcular o divisor de tensão? Mas o mais importante é saber como encontrar a equação do circuito divisor de tensão.
Para encontrar a tensão no resistor R3 devemos calcular o valor da corrente, que é igual o valor da tensão da fonte dividido pela soma de todos os resistores, e depois multiplicar pelo valor do resistor R3, que é onde queremos encontrar o valor da tensão, como mostrado abaixo:
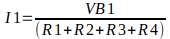
Mas observe que o valor da tensão de R3 é igual a:
VR3 = I * R3
Então substituindo a equação da corrente na equação onde queremos encontrar a tensão de R3, obtemos a equação do divisor de tensão:
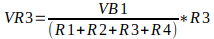
Isso é tudo, até um próximo post, e visite outras páginas da Wantronics:

