No post a seguir é feito o uso do Teorema de Thevenin, com a análise do circuito que foi apresentado no post anterior.

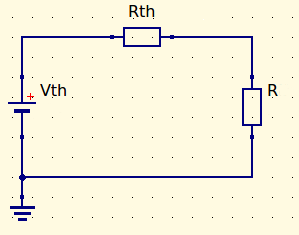
O Teorema de Thevenin ajuda na resolução de circuitos mais complexos, transformando um circuito com várias malhas em um circuito mais simples para análise.
O circuito que obtido após a aplicação do Teoremas de Thevenin, consiste de uma fonte de tensão, em série com um resistor equivalente de Thevenin, e o resistor que foi removido da malha para análise.

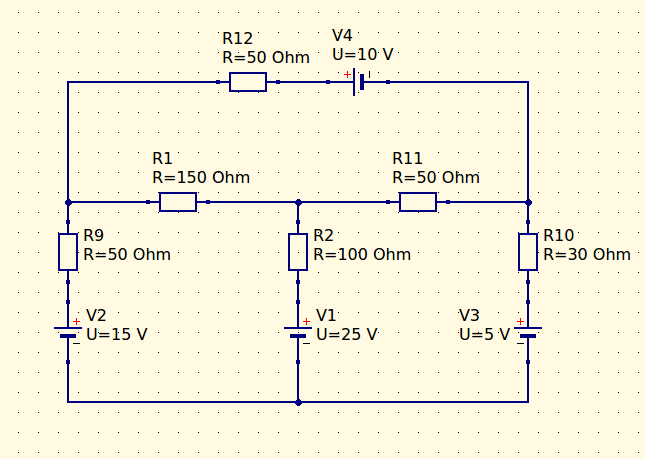
No Teorema de Thevenin é preciso calcular uma resistência equivalente de Thevenin, para o resistor da malha que estamos analisando, e para isso removemos o resistor do circuito e reduzimos todas as fontes de tensão a zero, ou seja, substituímos as fontes de tensão por curtos circuitos, e medidos a resistência entre os pontos onde foi removido o resistor. Veja como o circuito fica:

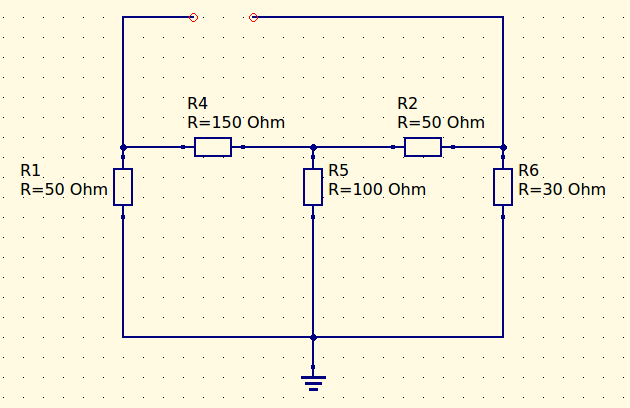
Para cálculo da resistência equivalente de Thevenin, neste caso em específico, será necessário a utilização da conversão de ∆ / Y, também conhecidos como redes de resistores Delta-Wye, caso contrário não será possível encontrar a resistência equivalente de Thevenin.
Na figura abaixo é mostra os dois circuitos para comparação e os cálculos para conversão de ∆ / Y.

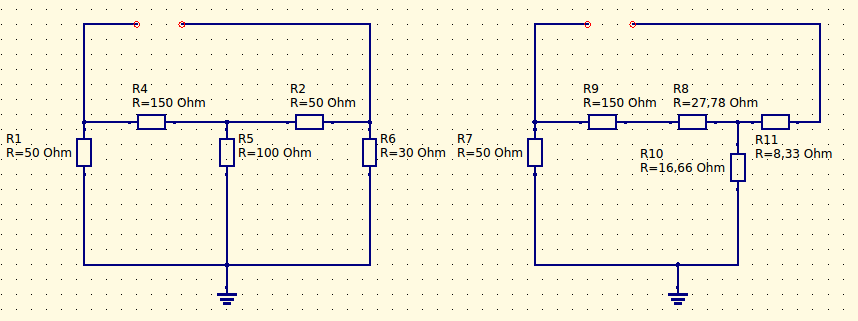
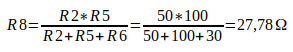
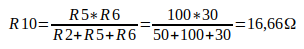
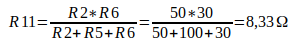
Agora ficou mais fácil encontrar a resistência equivalente de Thevenin, se reorganizar o circuito, obteremos [(R7 + R10) // (R9 + R8)] + R11. O valor de Rth = 56,81 Ohms.

Agora vamos encontrar a tensão de Thevenin, que é a tensão que que medimos entre os terminais do resistor que foi removido do circuito para análise.

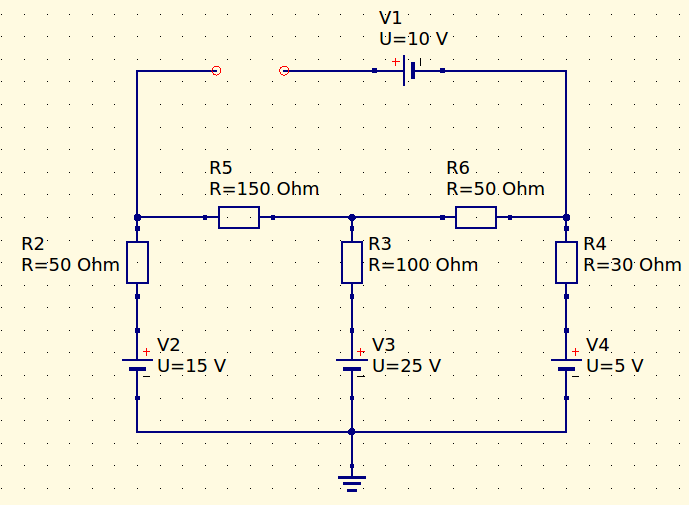
Muita atenção nesse momento, pode ser tentador adotar a tensão da fonte de 10 V como tensão do resistor, mas lembre-se que a tensão sobre o resistor é outra, vamos precisar encontrar a corrente das malhas do circuito abaixo, encontrar a tensão no ponto entre os resistores R2 e R5, e encontrar a ddp do ponto aberto.

Considerando apenas as malhas abaixo do ponto onde queremos encontrar a tensão, vamos obter o seguinte sistema de equações para encontrar I1 e I2.

300 * I1 – 100 * I2 = 10
-100 * I1 + 180 * I2 = -20
I1 = -4,54 mA e I2 = -113,64 mA
O sentido da corrente adotado para análise foi anti horário para duas malhas, e a resposta negativa indica que o sentido adotado está invertido em relação ao sentido real da corrente.

A queda de tensão no resistor R2 é igual a:
VR2 = 50 * 4,54 mA = 0,227 V, portanto a tensão no ponto entre os resistores R2 e R5 é de:
15 – 0,227 = 14,773 V
A tensão de Thevenin é igual a:
Vth = 14,773 – 10 = 4,773 V
I = V / (Rth + R)
I = 4,773 / (56,81 + 50) = 44,687 mA

Observem que a corrente não é a mesma que calculada no post anterior, que foi de 34,043 mA, mas agora vamos calcular a tensão a partir do ponto de terra, e seguir o fluxo de corrente no sentido correto:
25 – [100 * (113,64 mA – 4,5454 mA)] – (150 * 4,5454 mA)
25 – 10,909 – 0,68181 = 13,409 V
Vth = 13,409 – 10 = 3,409 V
I3 = 3,409 / (56,81 + 50) = 31,92 mA
Nos cálculos anteriores, a tensão que encontramos no ponto entre os resistores R2 e R5, é a tensão em relação a fonte de 15 V, e não tensão em relação ao referencial do circuito, e isso gerou uma diferença no valor da corrente

E assim obtemos o circuito equivalente de Thevenin para malha 3, é possível encontrar o mesmo valor de corrente que foi encontrado na análise anterior:

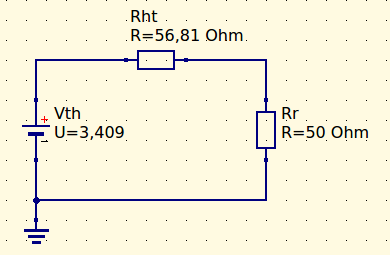
Para finalizar, foi feita a análise de apenas uma malha, as outras malhas ficam para o leitor treinar e verificar as correntes.
Até próximo post.